2.10. Lecture 9: Scale-free networks

Before this class you should:

• Read Think Complexity, Chapter 4, and answer the following questions:

  1. The probability mass function (PMF) plotted in Figure 4.1 is a normalized version of what other kind of plot?

  2. What is the continuous analogue of the PMF?

Before next class you should:

• Read Think Complexity, Chapter 5

Note taker: Kobe Barrette

2.10.1. Quickly Recapping Last Thursday’s Class:

• Introduce Generative Learning Models

  • Machine learning models that take inputs, synthesize the information, and create new data, e.g., image/video generation.

• Discussed the Watts-Strogatz (W-S) graph

  • This graph provided a hybrid between purely regular and random graphs to better represent ‘small world models’. To do this, the first step is to create a lattice graph with local connectivity. Then, the second step is to introduce some chaos by adding connectivity between random nodes. (Note: each random connection added requires a connection to be removed from the lattice).

• Introduced some metrics

  1. Average path length: The distance required to get from one node to another by following connectivity.

  2. Average clustering coefficient: This is the mean of local clustering, providing insight on how many ‘friends’ are connected together forming ‘cliques’.

• Introduced some functions/definitions

  1. pp.random.choice(): Computes choices randomly from a set of data, e.g., given dataset [A B C D] it may return ‘C’ from random selection.

  2. Node degree: Indicates the number of neighbors/edges a given node has.

2.10.2. Today’s Class:

• Introduce the concept of ‘Ego Networks’

• Discuss Julian McAuley (Professor at UC San Diego), as well as Jure Leskovec (Computer Scientist) and their machine learning research on ego networks using Facebook friend request data

• Compare and contrast Facebook data from SNAP (Stanford Network Analysis Project) to WS graphs using the same dataset

• Introduce the concept of ‘Degree’

• Discuss ‘Heavy-Tailed Distributions’ in PMF graphs

• Introduce ‘Barabasi-Albert’ (BA) Generative Models

• Briefly Introduce Cumulative Distribution

2.10.3. Ego Networks

An ego network consists of a focal node (ego) and its direct connections (alters), along with the ties between these alters. This structure models social relationships at different levels of connectivity.

An example of this would be to select professor Graham Taylor as the ‘ego’, then considering his immediate connections (alters) to be his colleagues, who also have connections such as work friends, then their high school friends, and so on. All of this forming a social network stemming from the single ‘ego’ generating an ‘Ego Network’.

2.10.4. Julian McAuley & Jure Leskovec

Professors McAuley and Leskovec are researchers in computer science, more specifically machine learning, who have experimented with social networks and explored the concept of ego network.

In a paper they wrote, Julian and Jure’s research allowed them to provide insight on ego networks by using Facebooks ‘friend request’ data as it’s source. They were able to form these social networks and address topics such as node clustering & mean path lenghts.

2.10.5. Synthesizing the data

2.10.5.1. Imports and Setup

Many of the imports are the same as seen in previous chapters. The main difference is introducing a function helper called download(), which is tasked with receiving a URL and retrieving it from the internet.

2.10.5.2. Approximate Algorithms

Since the Facebook dataset is quite extensive, it would be too costly (time consuming for the program) to use all of it during construction of WS graphs, as well as general data synthesis. Thus the concept of ‘Approximate Algorithms’ is a solution for this. This method is imported as ‘average_clustering’ from the ‘NetworkX’ library and takes a parameter called ‘trials’ which specifies an integer for which a random subset of the nodes will be selected as the sample. Another parameter in this method which can be used in some cases is ‘nodes’, which specifies a specific subset of nodes from the dataset to be evaluated.

The following code comprises definition of the helper functions used to compute estimated path length:

def sample_path_lengths(G, nodes=None, trials=1000):
    """Choose random pairs of nodes and compute the path length between them.

    G: Graph
    nodes: list of nodes to choose from
    trials: number of pairs to choose

    returns: list of path lengths
    """
    if nodes is None:
        nodes = list(G)
    else:
        nodes = list(nodes)

    pairs = np.random.choice(nodes, (trials, 2))
    lengths = [nx.shortest_path_length(G, *pair)
            for pair in pairs]
    return lengths


def estimate_path_length(G, nodes=None, trials=1000):
    return np.mean(sample_path_lengths(G, nodes, trials))

Note: the larger the value assigned to ‘trials’, the more nodes are considered, and selecting too large of a value may lead to a program cost similar to that of the entire dataset being used.

2.10.5.3. Analyzing the Results

Firstly, running the code with a trial of 1000 nodes selected from Facebook data, average_cluster & estimated_path_length yielded the following:

• average_cluster = 0.58

• estimated_path_length = 3.717

Interpreting these results, the actual average cluster from SNAP’s database was determined to be 0.61, which signifies the approximate algorithm provided accurate results. Similarly, the estimated path length was found to be lower than Stanley Milgram’s letter mailing findings, which had determined a path length of around 5.

2.10.5.4. Constructing & Comparing the WS graph

In order to appropriately compare the WS graph results to that of Facebook, the same variable should be used. Since the value of ‘k’ is rounded to an integer, the number of edges will differ slightly, here are the variable definitions:

n = len(fb)
m = len(fb.edges())
k = int(round(2*m/n))

• Using Ring Lattice (p = 0)

  • average_clustering = 0.733

  • estimated_path_length = 47.08

  Interpretation of the result: Using a ring lattice, the average clustering is slightly higher, and the estimated path length is much larger than Facebook’s data.

• Using a Random Graph (p = 1)

  • average_clustering = 0.005

  • estimated_path_length = 2.602

  Interpretation of the results: Using a random graph, both the average clustering and estimated path length are smaller than Facebook’s data.

Conclusion: both the ring lattice and random graphs with probability of randomness equal to 0 and 1, respectively, do not yield results that are similar to facebook’s data. However, from trial and error, a probability of p = 0.05 provides a close representation of Facebook’s data with average_cluster = 0.599, and estimated_path_length = 3.214.

2.10.6. Degree

The degree of a graph refers to the number of connections each node has. Similarly, the mean of these degrees can provide insight on how the social network is structured. By introducing the following helper function, the mean degree’s of Facebook and WS graphs can be determined:

def degrees(G):
    """List of degrees for nodes in `G`.

    G: Graph object

    returns: list of int
    """
    return [G.degree(u) for u in G]

By determining the mean of the resulting degree() method on both graphs, these resulted in 43.69 and 44.0, for Facebook and WS, respectively. These results proved to be almost equal to one another.

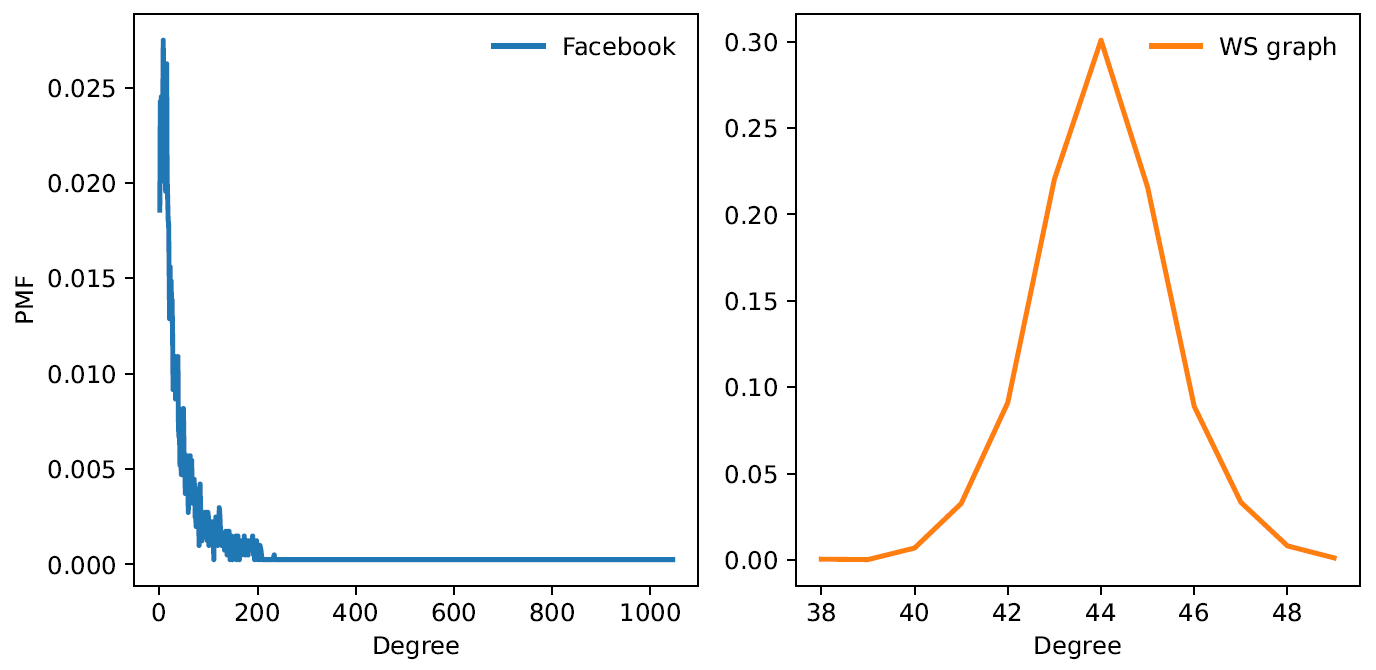
In order to vizualize what is happening ‘under the hood’, we import ‘PMF’ from empiricaldist. ‘PMF’ maps discrete quantities into probabilities, similar to a histogram. Applying this to each dataset, the resulting graphs are as follows:

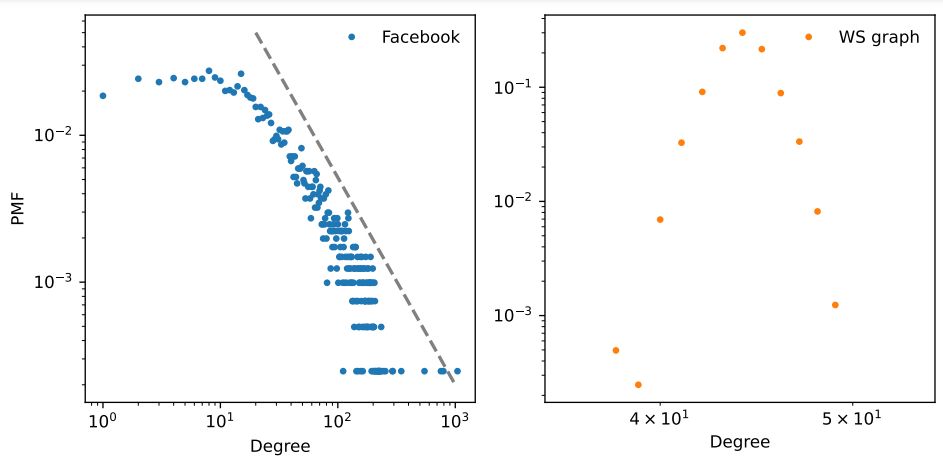
From this, it can be seen that the distribution is much different between each graph. Taking another step, we can apply logarithmic scales to the ‘x’ and ‘y’ axis and yield:

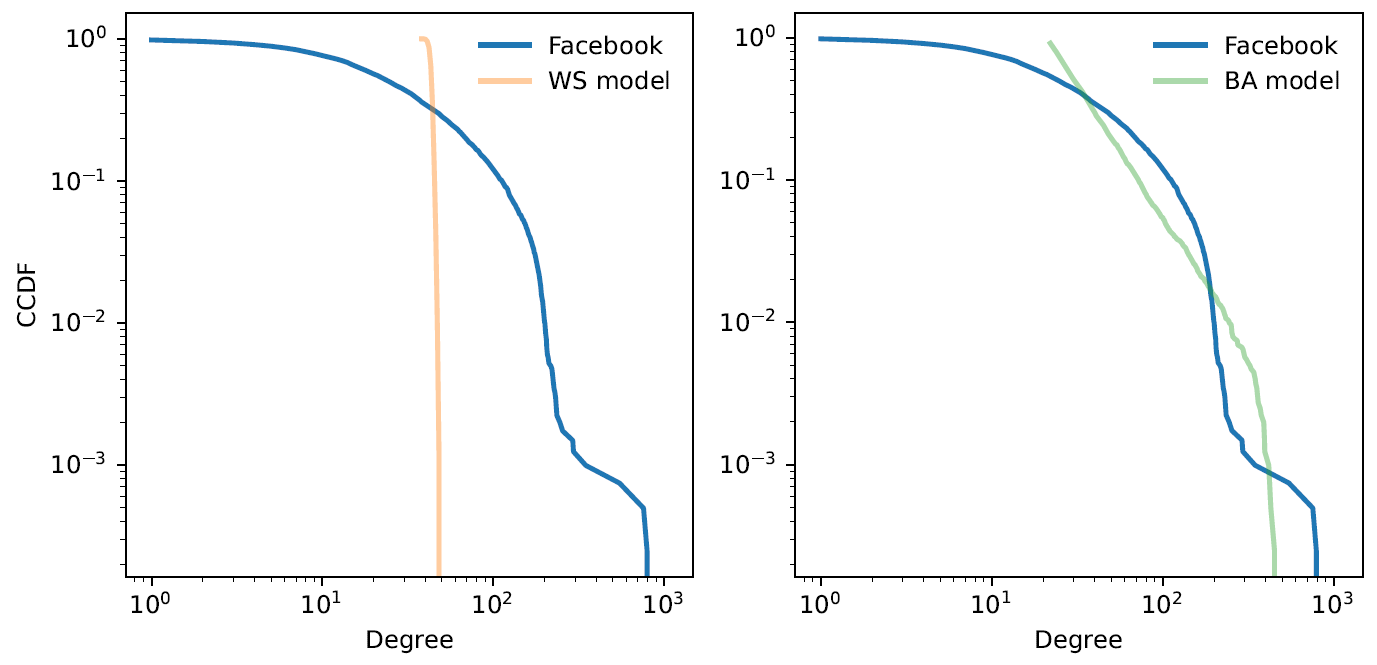
In the graph for facebook, the linear trend is known as a ‘powerline’ for which higher degree nodes tend to follow. This is known as ‘Heavy-Tail Distribution’ representing a small set of people who have an incredibly large subset of ‘friends’.

2.10.6.1. Heavy-Tailed Distribution

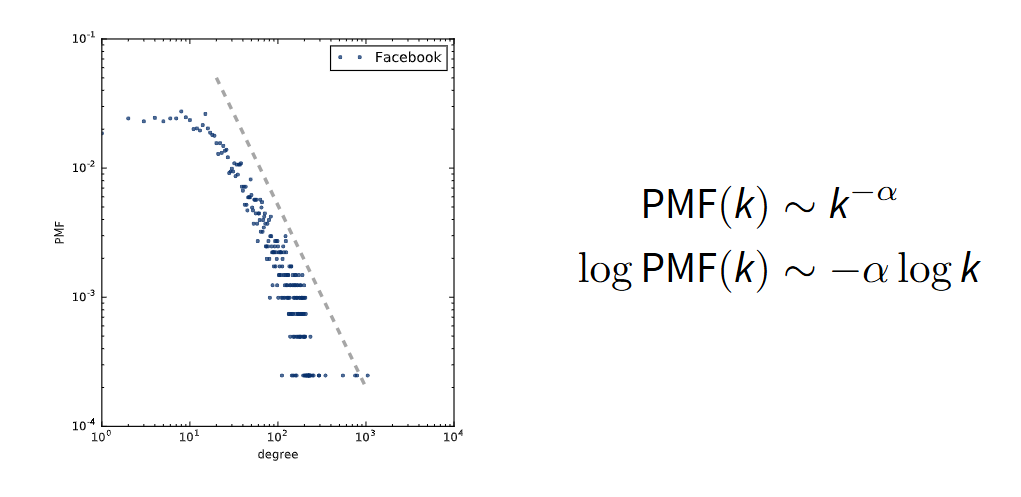
In a PMF, if there is powerline distribution, it can be modelled by the following equations:

A heavy-tailed distribution follows a power-law where a small number of nodes have significantly higher connectivity (degree) than others. This is evident in the log-log plot, where the degree distribution forms a nearly linear trend, indicating a power-law relationship.

2.10.7. Barabási -Albert (BA) Generative Model

Barabási and Albert propose a different generative model to represent ‘scale-free’ graphs. Their model differs as follows:

• Instead of starting with a fixed number of nodes and vertices, the model will begin small, and iteratively connect new indices one at a time, providing a slower approach as opposed to all at once.

• When a new edge is created, it is more likely to connect a vertex that already has a large numebr of edges, thus introducing the “rich get richer” effect.

The implementation between the BA generative model and ones seen previously follow a similar approach, with the exception being the nodes are added one at a time.

How does the “rich get richer” effect work?

Nodes are kept track of using some ‘ID’ and this ID is added to the set every time a connection occurs. Thus as new connections occur, nodes that are present in the set more often are more likely to have their ID randomly selected for connection, making them ‘more popular’.

When applying the BA model to facebook data and comparing, the results are as follows:

	fb	BA
mean path length	3.69	2.51
mean degree	43.7	43.7
standard degree	52.4	40.1
mean cluster coeff	0.61	0.037

From the table above, it can be noted that the standard degree of the BA model correctly represents Facebook model, however, the mean path length is slightly smaller and the mean cluster coefficient is much smaller, indicating this is a better generative model, but not perfect.

2.10.8. Cumulative Distributions

This is the final topic within the ‘Small-Scale Networks’ lecture which will be covered in detail in the following lab due to time constraints.

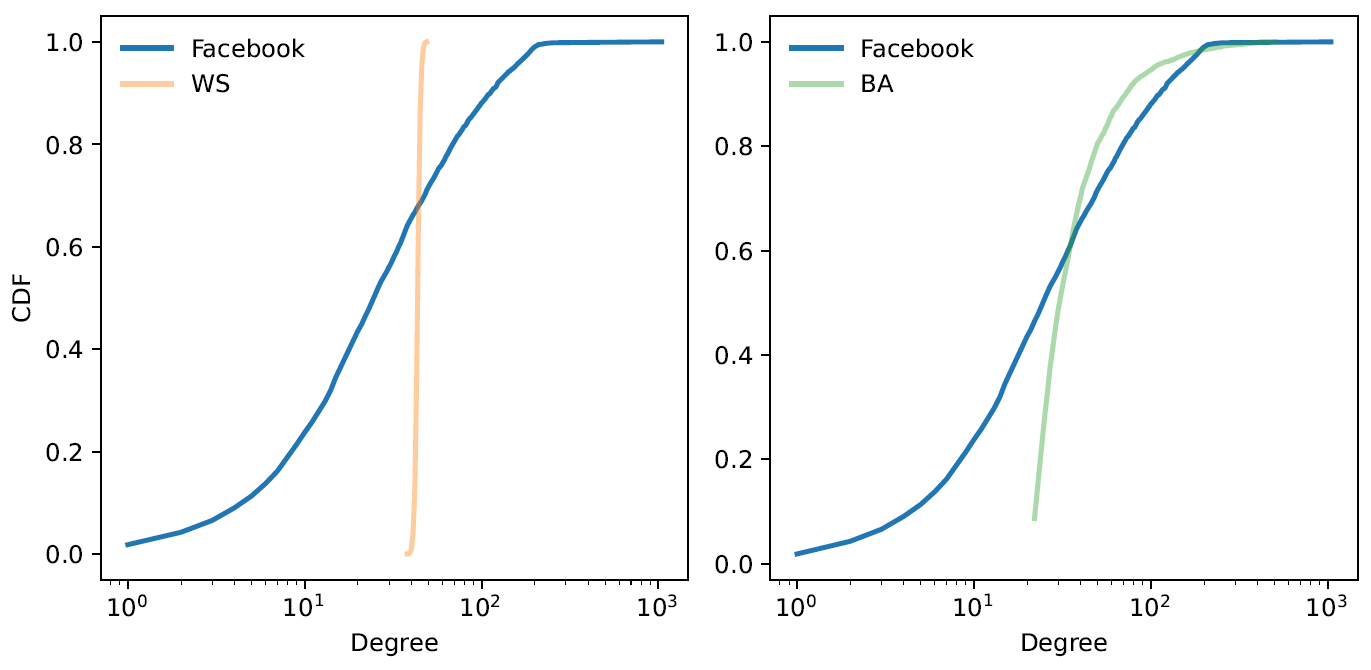
To summarize, cumulative distributions are a better way of vizualizing distributions. The function called ‘cumulative_prob’ takes a pmf and a variable ‘x’ and computes the total probability of all values less than or equal to ‘x’.

Using the Cdf() function from empiricaldist, the data discussed throughout this lecture can be plotted and visualized as follows:

The plot above uses a log-x scale.

The plot above uses a log-log scale.