2.9. Lecture 8: Small world graphs¶
Before this class you should:
Read Think Complexity, Chapter 3
Read the Wikipedia page on the Small-world Experiment https://en.wikipedia.org/wiki/Small-world_experiment
Read Watts and Strogatz “Collective Dynamics of ‘small world’ networks” http://www.nature.com/nature/journal/v393/n6684/full/393440a0.html
Before next class you should:
Read Think Complexity, Chapter 4, and answer the following questions:
The probability mass function (PMF) plotted in Figure 4.1 is a normalized version of what other kind of plot?
What is the continuous analogue of the PMF?
Note taker: Klaire McCarthy
Topics: Stanley Milgram + the Small World Experiment, Watts-Strogatz Graphs
ENGG3130 W25: 30 January 2025
Additional resources: Homework 3, Tutorial 3
2.9.1. Review Lecture 7: Graphs¶
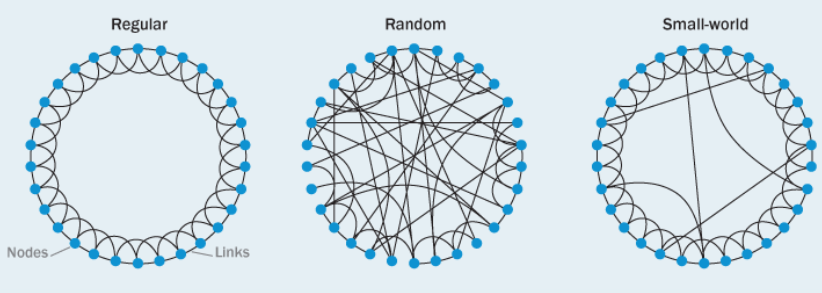
Regular graphs: all nodes have the same number of neighbours
Random graphs: edges are connected based on probability
Paths: the route (walk) taken from a given starting node to a given ending node, that does not revisit any previously visited nodes along the route (i.e. only visit each node in the route once)
2.9.2. Stanley Milgram + the Milgram Experiment¶
Stanley Milgram (1933 - 1984) was an American social psychologist who conducted two famous social experiments, The Milgram Experiment and the Small World Experiment. He also developed a technique for interactive social agents, Cyranoids.
The Milgram Experiment was a study of obedience to authority figures conducted in the 1960’s. It found that people (somewhat blindly) listen to authority figures. A participant was instructed by a scientist to administer electric shocks to a “learner” (learners were actors, no real shocks were administered) who acted a reaction to the pain of the shock. As a learner made more mistakes, the shock (and the learner’s reaction to it) increased.
The result of the experiment was that participants continued to shock the learners despite their blatant suffering, because the scientist had instructed the participant to do it. In conclusion, people’s obedience to authority figures can pose harm to individuals.
2.9.3. The Small World Experiment¶
Watched a YouTube video, ‘The Science of Six Degrees of Separation <https://www.youtube.com/watch?v=TcxZSmzPw8k>’_ by Veritasium.
The video describes a physical version of the Small World Experiment, where the goal was to have people mail 300 packages to Boston. The rule was that the packages had to be forwarded from person to person. The forwarding address had to be someone the sender knew on a first-name basis. The results of this experiment was that the average path length was 5.2, and of the 300 packages, only 18 reached their destination in the true spirit of the experiment (some people lived in Boston already, so their packages started at the final destination; others knew people living/working in Boston).
This experiment showed that any one person is connected to any other person by about 6 people (6 degrees of freedom/DOF). As clustering increases, path length decreases. Clustering in Watts-Strogatz Graphs is described below. Network traversal is most efficient if the graph has high clustering with a few random acquaintances to help jump around the network quickly. It’s by these random connections that the 6 degrees of freedom is possible. However, social media has dropped the DOF to about 4-5.
2.9.4. Watts-Strogatz Graphs¶
Watts and Strogatz proposed a simulated explanation of the small-world phenomena in 1998. A hybrid regular-random graph was developed and called the Watts-Strogatz (WS) graph, which combines two properties from two different graphs: high clustering (regular graphs) and low path length (random graphs).
An attribute of regular graphs is that they have high clustering. The clustering coefficient measures “cliqueishness”, which describes how the nodes are grouped. A high clustering coefficient indicates high cliquishness. The clustering coefficient quantifies the likelihood of two nodes connected to a common node being connected to each other. In social terms, this is the equivalent of your friends being friends with each other, too.
The path length of a random graph measures the average distance between a pair of nodes. Random graphs have low clustering and low path length due to their far-reaching connections.
A WS graph begins with a regular (lattice) graph of n nodes connected to k neighbours. A subset of edges are randomly chosen to be rewired by replacing their pre-existing lattice edge with a random edge, which connects it to a different neighbour. The probability of choosing a given node should be low, so as to maintain the lattice structure. The resulting WS graph has a high clustering coefficient (highly cliquey) with a low path length. The image below depicts the progression of a regular graph to a WS small-world network.
2.9.5. Attribution¶
Image from “Lecture 08b - WattsStrogatz” found in ENGG3130 CourseLink